IoTDB - RegionGroup均衡算法
背景
在不同的共识协议中,Leader 角色要比 Follower 角色承担更多的工作,包括
•CPU:Leader 要对操作进行编号,并且进行转发控制。
•网络IO:Leader 要将操作转发给剩余 R-1 个副本,输入是 1,输出是 R-1。
均衡各 DataNode 的 Leader 数量,能够均衡 CPU 和网络资源,以下使用贪心和最小费用最大流解决 RegionGroup-leader 的均衡分配问题。
贪心算法(初始化)
触发时机
每当有新的 RegionGroup 被创建时,调用贪心算法决定它的 leader。
算法流程
直接将 RegionGroup 的 leader 放置于目前持有 leader 数最少的 DataNode 上:
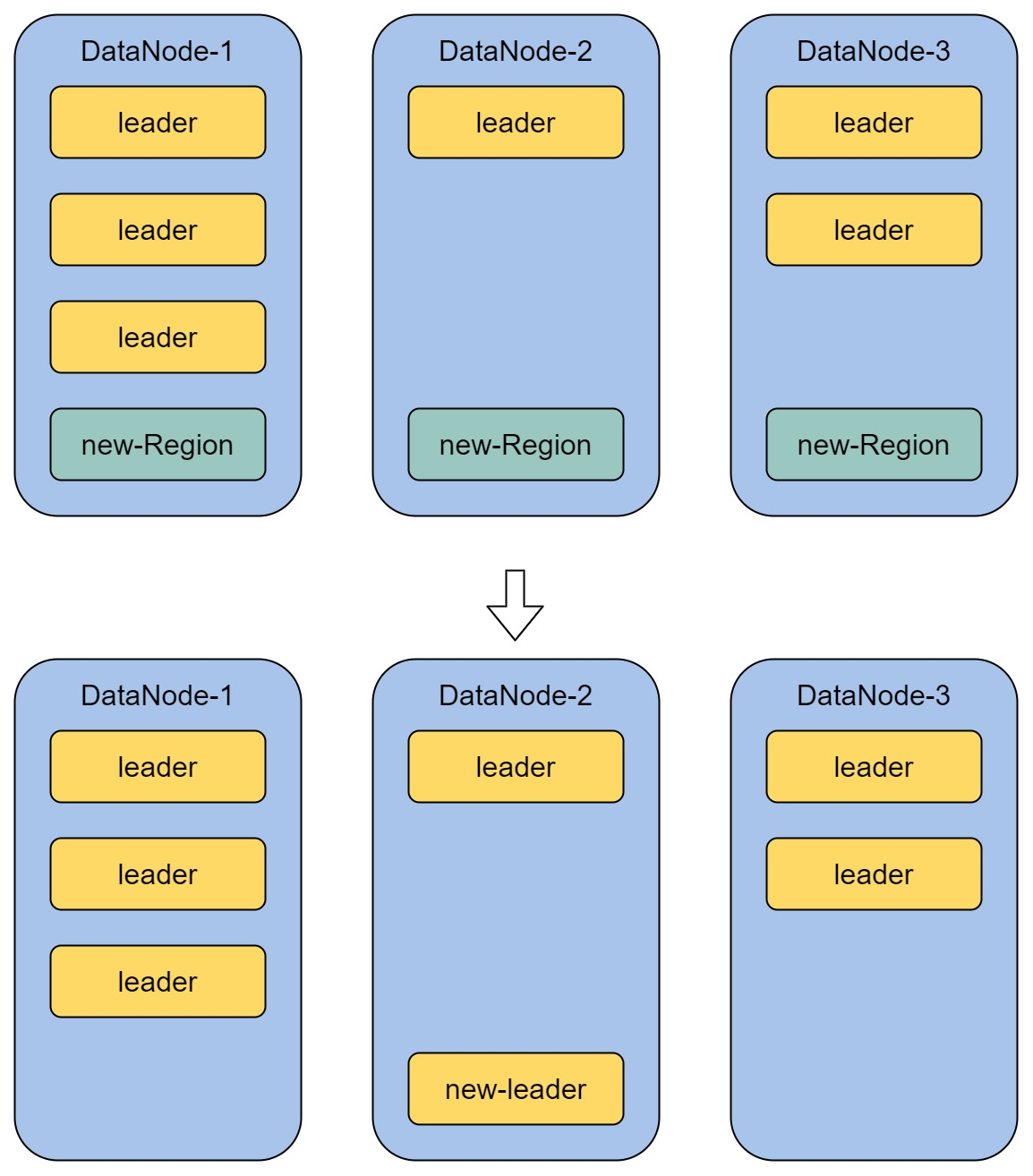
DataNode-2 持有的 leader 数最少(1个),因此将新 RegionGroup 的 leader 放置于 DataNode-2 即可。
算法分析
•可行性:新建的 RegionGroup 尚未持有任何共识日志,因此总能指定任意一个 Region 为 leader
•最优性:将 leader 放置于负载最低的 DataNode 上总是最优的
最小费用最大流算法(调整)
触发时机
集群运行中,ConfigNode-leader 周期触发(如每隔 10s 触发一次)最小费用最大流算法,以调整集群各个 RegionGroup 的 leader 分布。
集群状态是不可把控的,如 DataNode 随时可能切换状态,因此调整算法需要周期触发。
示例
3 replica,5 RegionGroup,3 DataNode 集群的示例网络
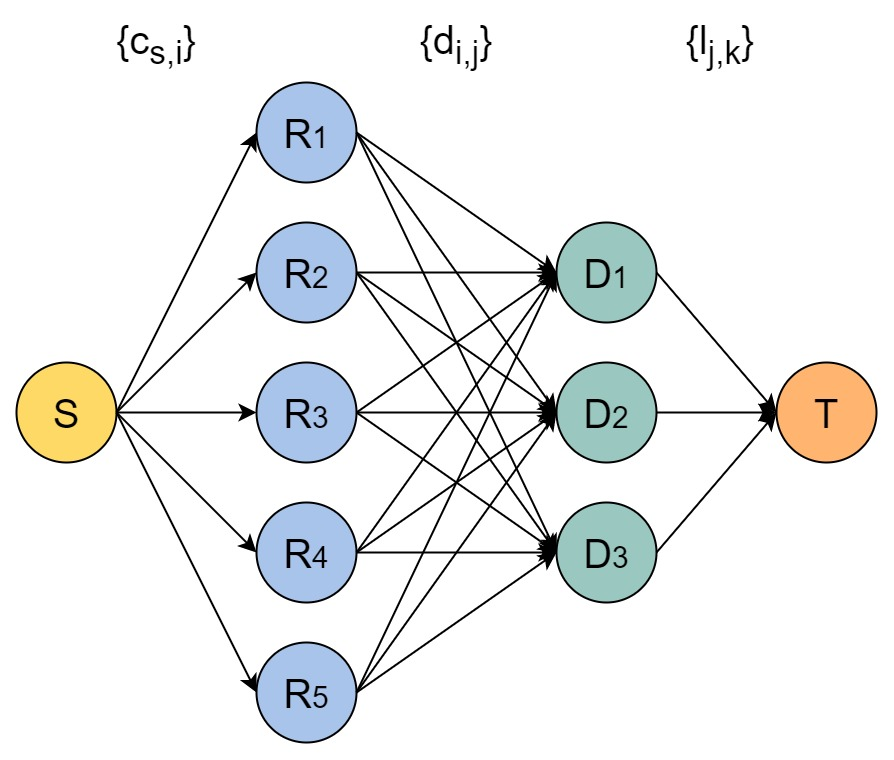
算法需要为每个 RegionGroup 决定唯一的 DataNode,将该 RegionGroup 的 Leader 置于该 DataNode 上,即二分图匹配问题。
网络定义
定义流量网络G={V, E} 如下
点集定义
本算法对流量网络的点集定义为V={S}、{Rn}、{Dm}、{T}的并集:
•S: 流量网络源点
•{Rn}: RegionGroup 点集,其中Ri 即{RegionGroup}i
•{Dm} : DataNode 点集,其中Dj即{DataNode}j ,{Dm}只包含 Running 状态的 DataNode
•T: 流量网络汇点
边集定义
流量网络中每条边具有两个属性:
1.容量:边能承载的最大流量
2.代价:边通过单位流量需要付出的代价
3.本算法对流量网络的边集定义如下:

算法分析
显然,不存在合适的贪心算法能让 leader 调整问题取最优解。
将 leader 调整问题转化为二分图匹配问题,最小费用最大流算法总能给出二分图匹配的最优解:
1.匹配结果中各 DataNode 拥有的 leader 数总是几乎一致的(差值不超过 1)理由:负载边的代价满足琴生不等式
2.各 RegionGroup 尽可能不切换 leader理由:切换 leader 产生 1 代价
3.若切换 leader 能让 DataNode 持有的 leader 数量更加均衡(极差减小),一定切换
理由:$\forall\ k_1 > k_2,\ \Delta(i,j)\ \leq\ 1\ \leq\ g(k_1) - g(k_2)$
调整算法所做的 leader 切换决策将导致 ConfigNode-leader 命令某些具体的 RegionGroup 执行 transferLeader 操作,这些操作并不都能成功,但每个成功的操作一定能优化集群负载分布。因为决策总是将 RegionGroup-leader 从负载高(持有 leader 多)的 DataNode 调度给负载低(持有 leader 少)的 DataNode。
可扩展性分析
倾斜集群
实际生产环境中,DataNode 持有的配置往往是有差异的,可以通过限制对应**负载边**{lj,t} 的总容量,达到控制某个 DataNode 持有 leader 数量上限的效果
多主协议
若某个共识协议使 RegionGroup 必须配备两个或以上的 leader,只需对应修改**容量边**{cs,i}配置即可
为什么不采用贪心算法
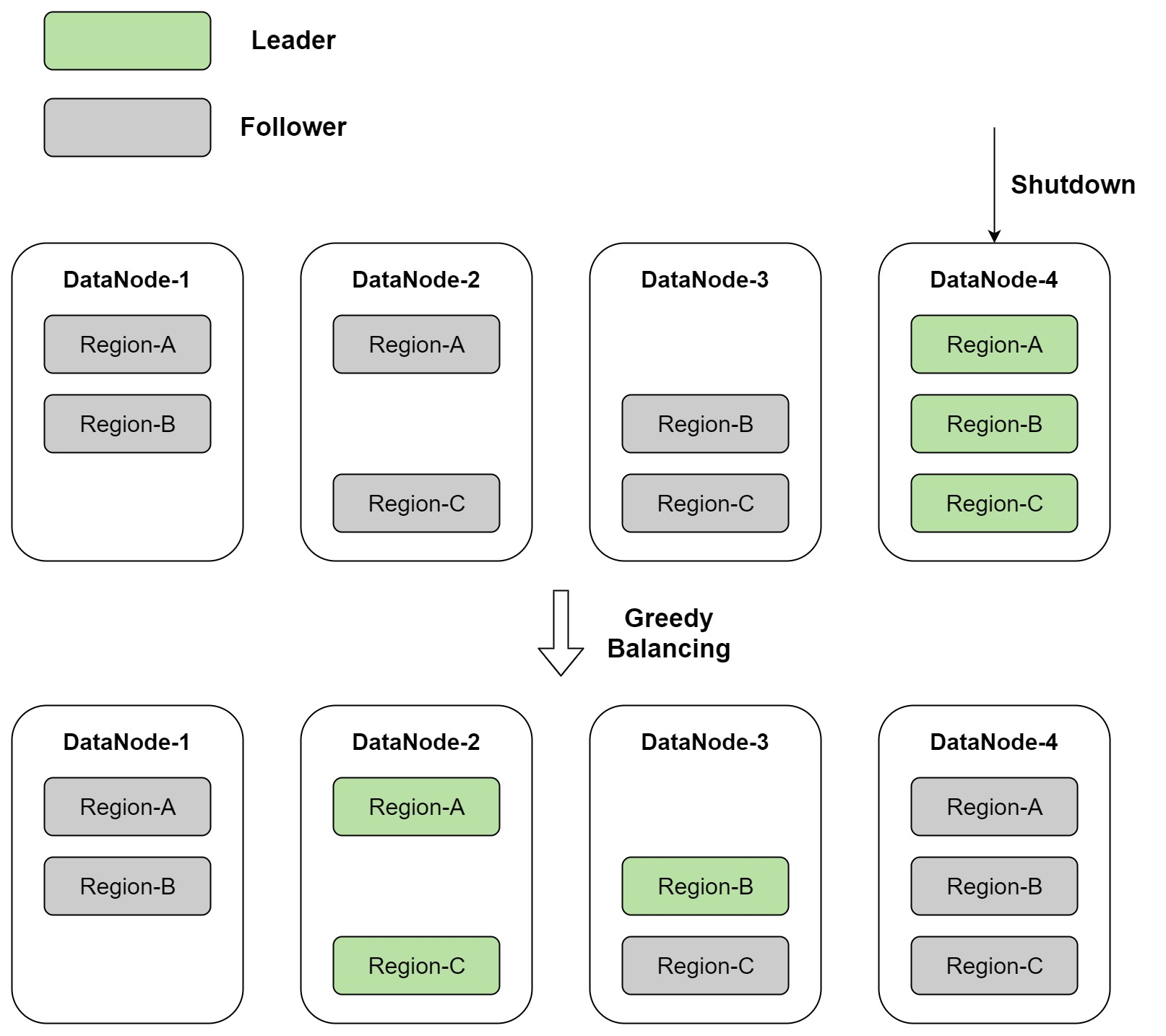
图示有三个 RegionGroup:
•A: {1, 2, 4}
•B: {1, 3, 4}
•C: {2, 3, 4}
•贪心算法流程如下:
1.当前三个 RegionGroup 的 leader 都在 DataNode-4
2.DataNode-4 宕机
3.RegionGroup-A 的 leader 切换至 DataNode-2
4.RegionGroup-B 的 leader 切换至 DataNode-3
5.RegionGroup-C 的 leader 切换至 DataNode-2
6.在上述流程中,3. 与 4. 的决策是可能发生的,因为决策时 DataNode-2 与 DataNode-3 都是可行选项。进而得不到此情形下 leader 的均衡分布,而一个可行的均衡分布是:{A->1, B->3, C->2}