大数据流上的Heavy Hitters
看了一些Flink RocksDB状态后端热key探测的研究,其中不可避免地要解决Heavy Hitters问题,简单记录。
Heavy Hitters(频繁项)以及它衍生出来的Top-K(前K最高频项)是大数据和流式计算领域非常经典的问题,并且在海量数据+内存有限+在线计算的前提下,传统的HashMap + Heap-Sort方式几乎不可行,需要利用更加高效的数据结构和算法来解决。好在众多前人对Heavy Hitters问题进行了深入的研究,并总结出了很多有效的方案。
两种主流的Heavy Hitters算法类别,即:
基于计数器(Counter-based)的方法
基于略图(Sketch-based)的方法
基于计数器的方法
Majority问题
数组中有一个数字出现的次数超过数组长度的一半,请用尽量快的方法找出这个数字。
思路很简单:遍历数组,如果前后遇到的两个数不相等,就将这两个数消去,最终剩下的那个肯定是出现次数超过一半的那个数。具体到操作上,可以设定一个候选值与一个计数器,在遍历过程中,如果遇到的数与候选值相同则增加计数,不同则减少计数。候选值的计数减为0时,表示它肯定不是所求的结果,选取下一个数作为候选值,直到遍历完毕。
Misra-Gries算法
将Majority问题推广,就会变成:
数据流中一共有m个元素,请找出出现频率超过m / k的k - 1个元素。
Majority问题就是上述问题k = 2时的特例。而套用上面的计数器思路,就是Misra-Gries算法,该算法早在1982年就提出了。
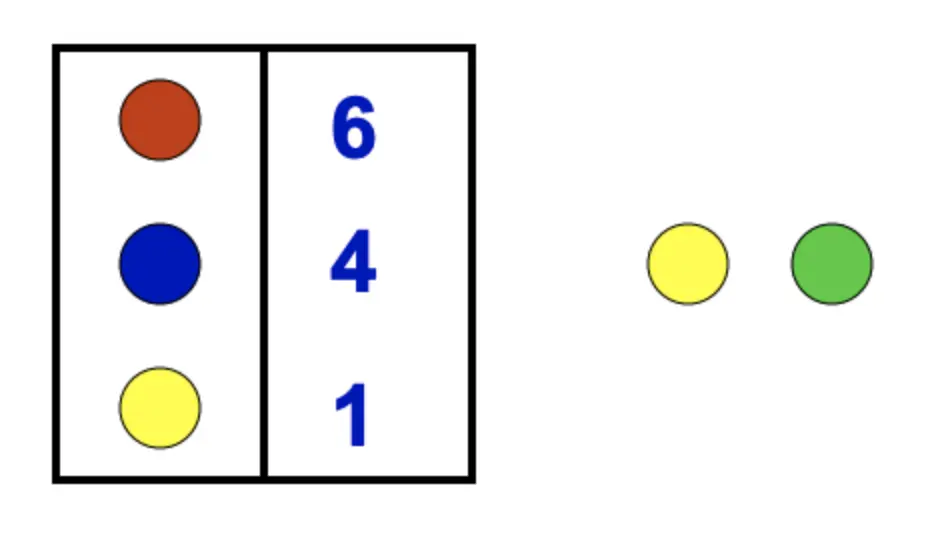
如图所示,维护k - 1个候选值与计数器的集合:
如果元素在集合中,将其对应的计数器自增;
如果元素不在集合中且集合未满,就将元素加入集合,计数器设为1;
如果元素不在集合中且集合已满,将集合内所有计数器自减,计数器减为0的元素被移除。
Misra-Gries算法可以利用O(k)的空间对元素j的出现频率 fj 做出如下的估计:
- fj - (m - m’)/k <= fj <= fj
(其中fj是j的真实出现频率,m'则是集合中的所有计数器之和)
计数器自减只会发生在集合满时,且触发计数器自减的那个元素也不会被统计到,所以相当于少统计了(k - 1) + 1 = k个元素。也就是说,计数器自减的操作最多能发生(m - m’)/k轮——即fj与 fj 之间的最大差值。由此可以总结出:
-
Misra-Gries算法对元素出现频率的估计总是偏低的;
-
k越大(即计数器的集合越大),频率的估计误差越小;
-
最终结果能够保证没有假阴性(false negative),即不会漏掉实际频率高于m / k的元素。但可能会出现假阳性(false positive),即混入实际频率低于m / k的元素。
Lossy Counting算法
流程如下。
- 将数据流划分为固定大小的窗口。
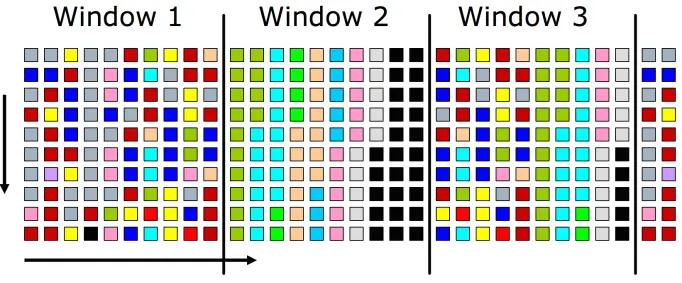
- 统计每一个窗口中元素的频率,维护在计数器的集合中。然后将所有计数器的值自减1,将计数器减为0的元素从集合中移除。
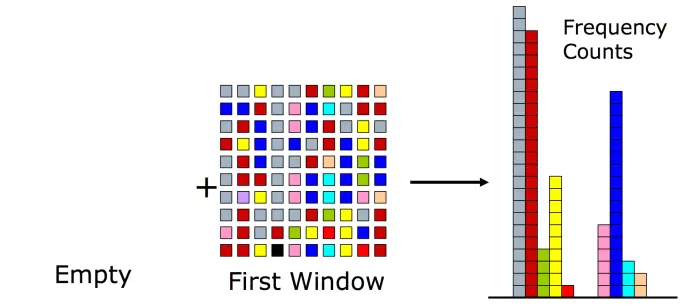
- 重复上述步骤,每次都统计一个窗口中的元素,将频率值累加到计数器中,并将所有计数器自减1,并将计数器减为0的元素从集合中移除。
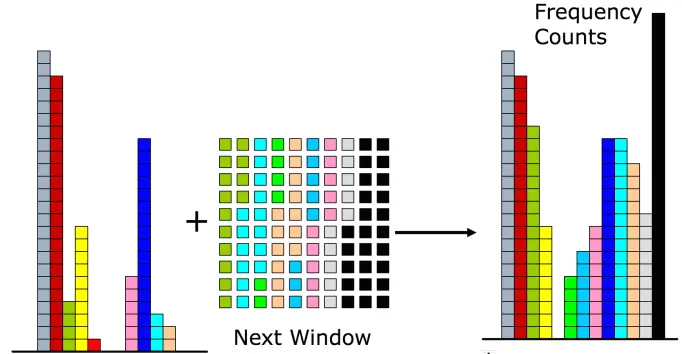
在窗口大小为1/ε的情况下,套用Misra-Gries算法的误差分析思路,容易得出Lossy Counting算法对元素出现频率的估计同样是偏低的,会出现假阳性,且误差在εm的范围内。换句话说,如果我们希望得出频率超过Fm的所有元素(F是个比例,如20%),那么我们最终得到的是频率超过(F - ε)m的结果。原作论文内建议F大约设为ε的10倍。
论文也指出Lossy Counting算法的空间占用为O(1/ε · log εm),可见它是以比Misra-Gries算法更多的空间作为trade-off换来了更低的误差。
为什么有实用价值?根据著名的Zipf’s Law ,元素在数据流中的分布往往高度倾斜,少数频繁出现的元素占据了数据流中的大部分空间。所以,即使它们是不精准的,但仍然能够给出大致正确的、有意义的统计结果。
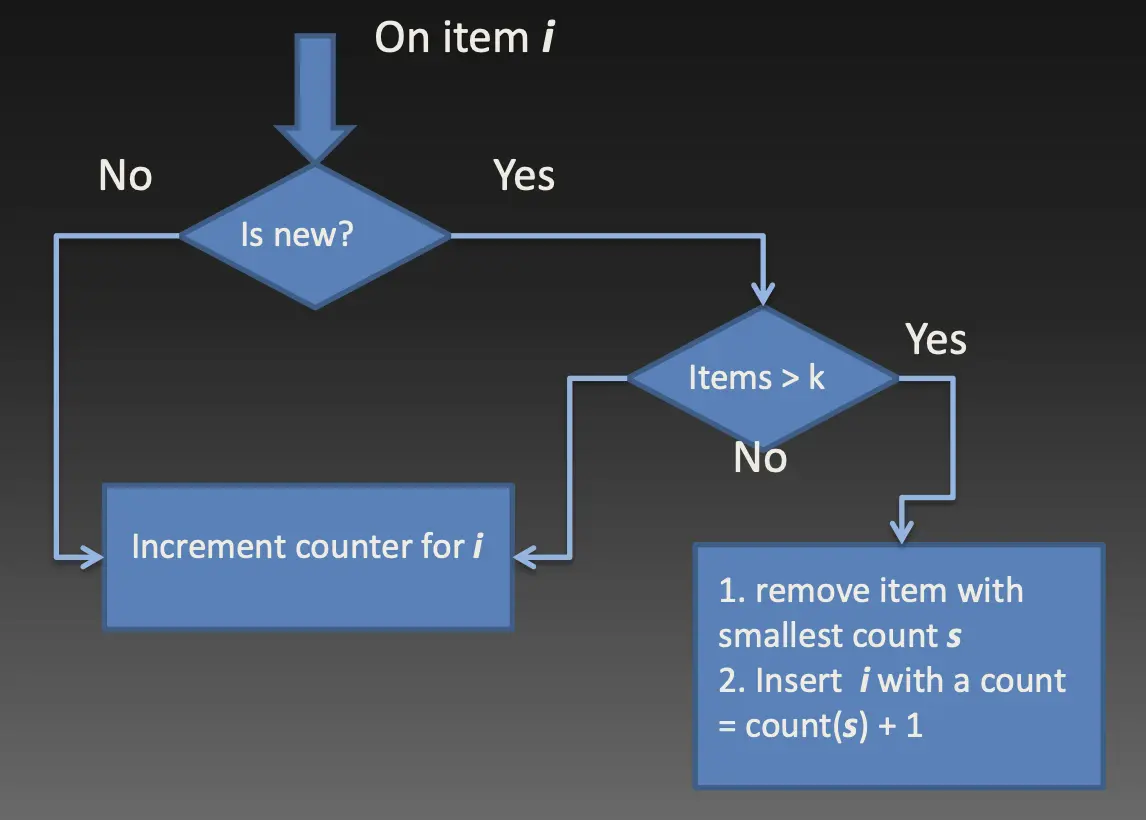
Space Saving算法
本质上是Misra-Gries和Lossy Counting算法的折衷,也是目前应用最广泛的Heavy Hitters算法之一。它维护k = 1/ε个候选值与计数器的集合,操作流程如下图所示。
-
如果元素在集合中,将其对应的计数器自增;
-
如果元素不在集合中且集合未满,就将元素加入集合,计数器设为1;
-
如果元素不在集合中且集合已满,将集合内计数器值最小的元素移除,将新元素插入到它的位置,并且在原计数值的基础上自增。(这里维护计数值最小的元素可以用传统的堆)
Space Saving算法构建在Misra-Gries算法的基础上,且只有第三种情况的处理方式是不一样的——借鉴了Lossy Counting的合并思路。除了只需要O(k)的空间之外,这样操作的好处是,所有计数器的和一定等于数据流的总元素数m(因为不需要做减法,只需要自增),且那些没有被移除过的元素的计数值是准确的。容易分析得出:
-
集合中最小的计数值min一定不会大于m / k = εm,同时能够保证找出所有频率大于εm的元素;
-
元素出现频率的估计误差同样在εm的范围内,不过会偏高;
-
Space Saving算法也有假阳性的问题,特别是在非频繁项集中位于流的末尾时。
Space Saving算法在贴近实际应用的Zipfian数据集上的benchmark如下图所示,可见与其他算法相比,无论在准确率方面还是效率方面都几乎是最优的。
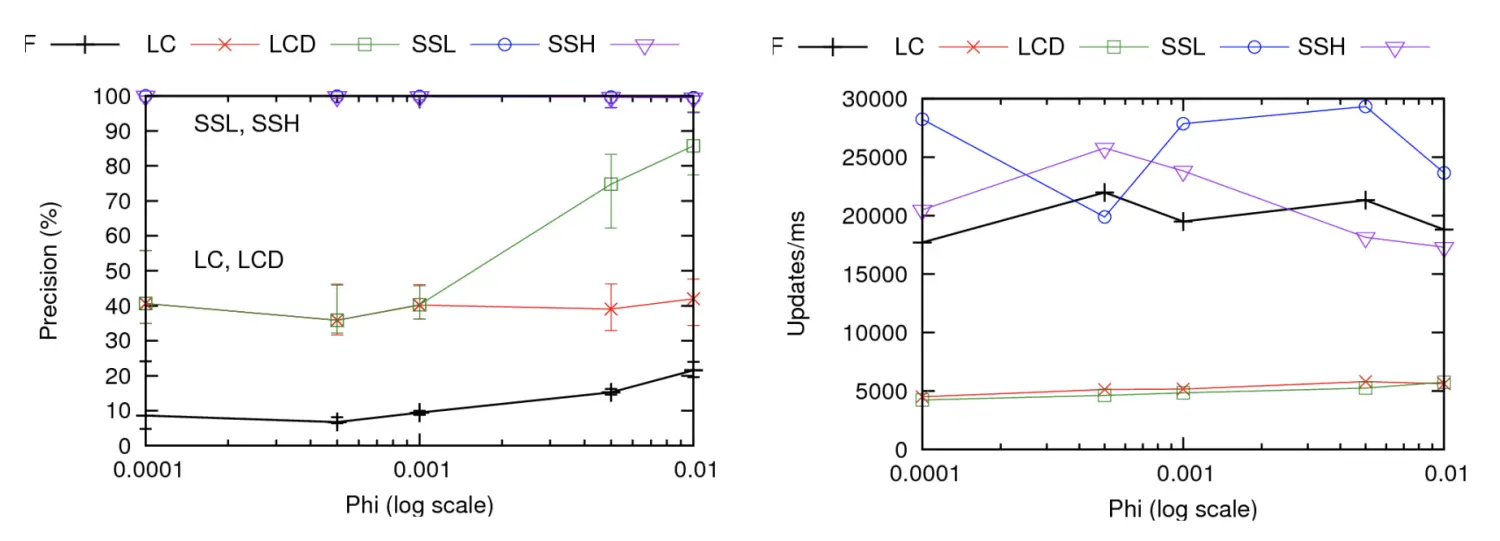
在大数据相关的组件中,Space Saving算法应用比较广泛,如Apache Kylin中的Top-N近似预计算特性就用到了该算法。又例如ClickHouse函数库中的anyHeavy函数,它能够返回数据集中任意一个频繁项。它们使用的都是并行化的Space Saving算法,能够显著提升多线程环境下的计算效率。
基于略图的方法
略图(Sketch)就是能够大致准确地描述一份数据集的摘要。当数据量非常大时,往往不能直接放入内存中,普通的查找树、哈希表等受制于数据规模。略图以精准度作为trade-off换来了时间、空间效率的极大提升,也使得解决大数据上的Heavy Hitters以及其他很多问题成为可能。
概率性数据结构(probabilistic data structure)有不少都采用了略图的思想,如布隆过滤器(Bloom Filter)借助位图与多个哈希函数来非常高效地判断集合中元素的存在性。 Count-Min Sketch与Count Sketch 本质上也是布隆过滤器思想的延续。
Count-Min Sketch
其数据结构由两部分组成:
-
一个宽度为w,深度为d(即d行w列)的二维整数数组,初始化为全0;
-
d个互相独立的哈希函数h1…hd,其哈希空间均为[1…w]。
观察数据流,当数据流中元素j出现时(可以出现1次,也可以连续出现c次),将j分别用哈希函数h1…hd映射到二维数组中每一行的对应位置,并将该位置的值加上c。如下图所示,可以看出,Count-Min Sketch非常类似于扩展到d维并且加上了计数功能的布隆过滤器。
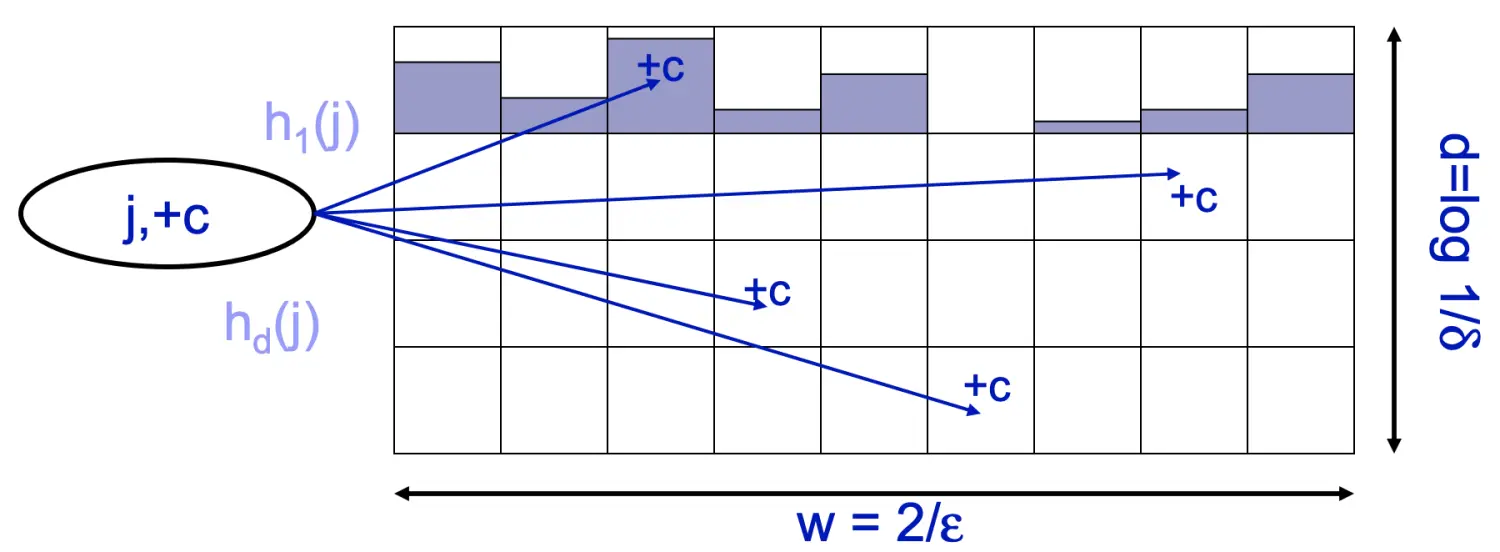
如何估计一个元素j的大致出现频率 f[j] ? 直接取元素j对应的所有哈希桶中,计数值最小的那一个。即:
f[j] = mink CMS[k][hk(j)]
为了保证一定的精准度,w和d的取值:
定义精度参数为ε,误差概率参数为δ(两者都是很小的正数),有:
w = 2/ε, d = log 1/δ
ε、δ关系:
P{ f[j] <= f[j] + ε f 1 } >= 1 - δ
在至少为1 - δ的概率下, Count-Min Sketch对任意一个元素j估计的出现频率与其真实频率的误差小于所有元素真实频率之和的ε倍。这个结论可以用马尔可夫不等式来证明
由于哈希冲突的存在,Count-Min Sketch给出的频率估计肯定是偏大的(即_f[j]_ >= f[j])。在输入数据量足够多的情况下,选择最小的频率计数值就意味着哈希冲突最少,亦即更接近真实的频率值。相反,对于很少出现的元素,表现就会比较差。
如何用Count-Min Sketch解决Heavy Hitters问题? —— 使用K个元素的最小堆维护Top-K,每更新一个元素的计数,就同时更新到最小堆,并随时移除频率过小的元素。
Apache Spark在spark-sketch子模块中实现了包括Count-Min Sketch在内的多种略图结构,并应用在CountMinSketchAgg聚合函数以及DataFrame的数据统计中。PostgreSQL也有一个Count-Min Sketch插件,专门用于近似计算Top-K。
Count Sketch
本质上是Count-Min Sketch的一般化形式。除了w*d的二维数组和d个哈希函数之外,还有另外一组哈希函数g1…gd,且它们的哈希空间只有{1, -1}两个值。另外,g1…gd取{1, -1}的分布必须是随机且均匀的,也就是说E[g(j)]=0。
当数据流中元素j出现c次时,将j分别用哈希函数h1…hd映射到二维数组中每一行的对应位置,并将该位置的值加上c*g(j),如下图所示。
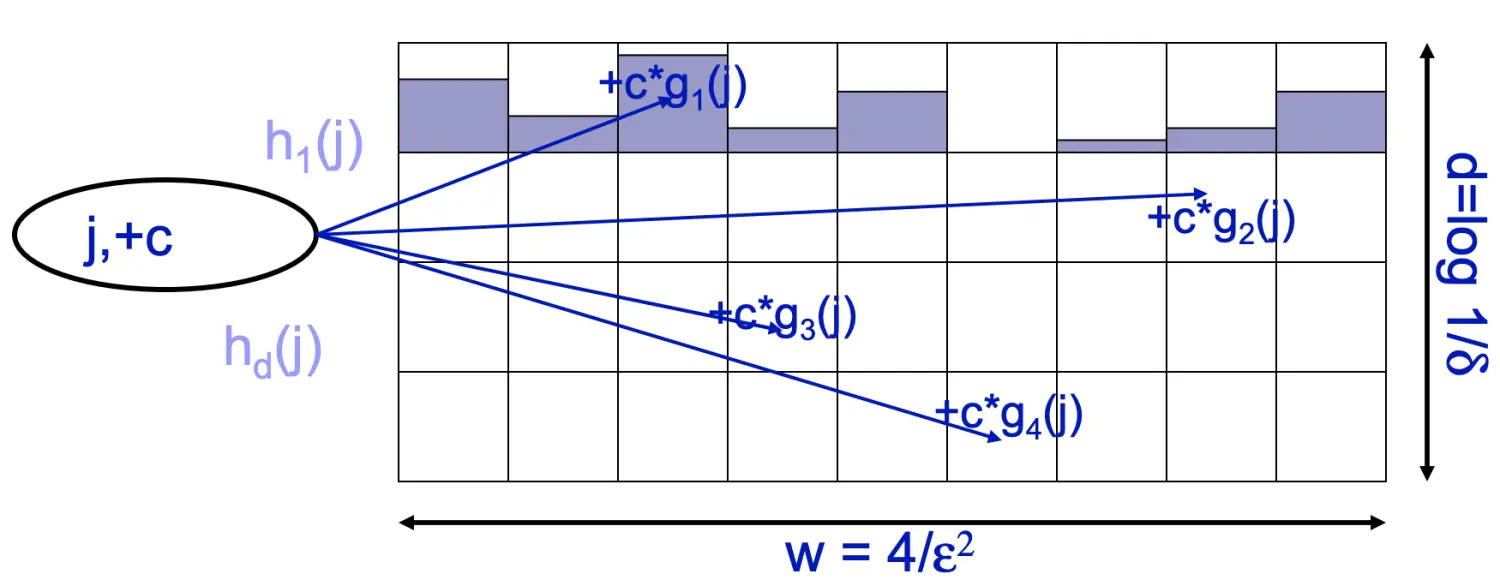
g1…gd哈希函数是Count Sketch与Count-Min Sketch的最大不同点,可以部分抹去Count-Min Sketch中的只加操作带来的正误差,因此估算 f[j] 时不必再取元素j对应的所有哈希桶中计数值最小的那一个了。取中位数,即:
f[j] = medianj CS[k][hk(j)] * gk(j)
Count Sketch的ε、δ两个参数与估计误差之间有如下的关系(切比雪夫不等式证明):
P{ f[j] - ε f-j 2 <= f[j] <= f[j] + ε f-j 2 } >= 1 - δ
由上可知,Count-Sketch给出的频率估计有可能偏大也有可能偏小,但是它用更多的空间(w ~ O(1/ε2))换来了比Count-Min Sketch更严格的误差界限。
使用Count Sketch解决Heavy Hitters问题的思路与Count-Min Sketch相同。